ÁREA DEL CUCHILLO DEL ZAPATERO (ARBELOS)
Arquímedes de Siracusa, propone en el libro de los lemas otro problema interesante.
Sea ABC un semicírculo. Por el punto B se traza una perpendicular BD al diámetro AC y sobre los segmentos AD y DC como diámetros se construyen dos semicírculos AFD y DHC. El área AFDHCB de las dos hoces obtenidas (Arquímedes lo llama arbelon, de árbelos, que es como se llama en griego al cuchillo del zapatero) es igual al área del círculo de diámetro DB. Demuéstralo.
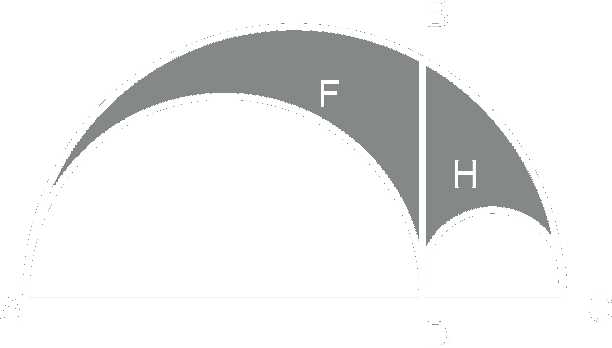
Sólo hace falta recordar el Teorema de Pitágoras y que los segmentos trazados desde cualquier punto de una semicircunferencia hasta los extremos del diámetro forman un ángulo recto (una semicircunferencia es un arco capaz de 90º).